公元前100年
-
勾股定理
3
《周髀算经》
“周三径一”
3.1416
刘徽与“割圆术”
圆内接正3072边形
3.1415926
祖冲之
圆内接正24576边形
以割圆之术， 破数学之界
割圆术：
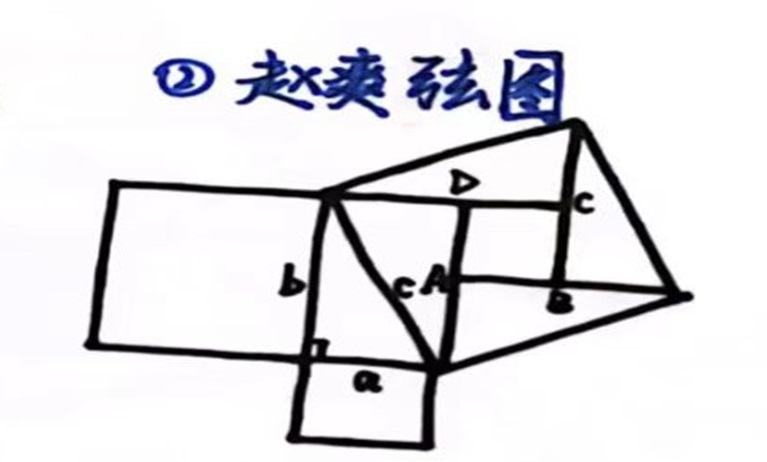
割圆术：
于方圆之间，镌刻数学的不朽传奇
割圆术以极限思维为刃，在数学的广袤天地中披荆斩棘，它凭借着精妙绝伦的构思，将无限与有限巧妙交融，开创了古代数学对圆周率精确求解的先河，是华夏数学智慧的卓越典范。
- 刘徽：“割之弥细，所失弥少，割之又割，以至不可割，则与圆周合体而无所失矣”
- 祖冲之：π的两个分数形式的近似值：约率22/7和密率355/113
天元术
祖率
比例算法
方程术
增乘开方法
正负开方术
大衍求一术
四元术
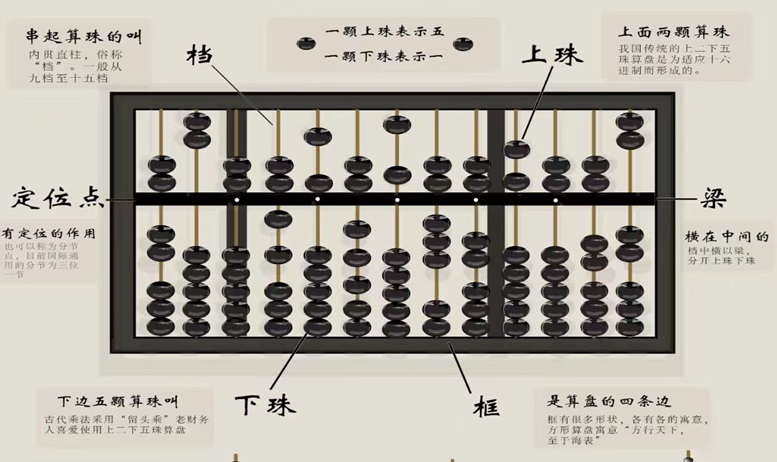
十进位值制
中国至迟在商代已经采用，
比古埃及早1000多年。
杨辉三角
中国1050年构造出。法国数学家
布莱士·帕斯卡1653年才记载了此三角形。
天元术
金元时期创立天元术。欧洲直
到17世纪才由笛卡尔等数学家
建立类似，中国领先300年
全球名人论道
大咖评点！ 中国古代数学 的辉煌
“历史上一个国家计算得出的圆周率准确程度，可以作为衡量这个国家当时数学水平的标准”。中国南北朝时期的祖冲之将圆周率计算到小数点后七位数，在当时世界上无人能及。
康托
19世纪德国伟大的数学家
中国的数学跟西方的数学实际上是数学的两个大的思想。他还发表了《中国古代数学对世界文化的伟大贡献》一文，纠正了国际上通常认为中国古代没有系统数学理论、对数学发展影响不大的偏见。
吴文俊
“科学巨匠”
中国的数学在魏晋南北朝以前在世界古文明里面有一定的贡献，不算差，但主要是以应用为主。在隋唐到宋朝末年，中国数学的有些方面比西方进步，尤其宋朝可以讲是比欧洲更先进一点。
丘成桐
数学大师
中国 珠算
九章 算术
周髀算经
赵爽弦图
商 高
贾 宪
张 衡
从问题到答案的 跨越
古代数学家的 灵魂叩问与智慧回响
别慌，看我“割圆术”，把圆内接正多边形边数疯狂增加，用多边形面积就能无限接近圆面积，圆周率近似值3.1416这不就有了！
莫急莫急，沿着刘徽前辈的“割圆术”接着算，算到圆内接正24576边形，成功把圆周率精确到小数点后七位，就在3.1415926和3.1415927之间啦！沿用刘徽“割圆术”，算到圆内接正24576边形，将圆周率精确到小数点后七位，在3.1415926和3.1415927之间。
放着我来！独创“正负开方术”，随乘随加，从低次幂项一步步往高次幂项算，任意次方程正根都能轻松拿下！
瞧我的“四元术”，天、地、人、物四元代表四个未知数，再用消元法，多元高次方程组瞬间被轻松化解！
古智慧 今应用
千年沉淀在当代社会的 多元应用
穿越千年历史长河，中国古代数学成就熠熠生辉。
在现代社会续写辉煌，且看这奇妙融合。
勾股定理
中国珠算
中国剩余定理